During my last quarter at Rose-Hulman I took a great class called ECE481 - Electronic Music Synthesis. In it, we discussed a lot of concepts used to synthesize music, including additive and destructive synthesis, FM synthesis, the Karplus-Strong algorithm, and various post-processing and mixing techniques.
As a final project for the course we were asked to create a song using some of the techniques we learned about. For my project, I chose to synthesize the solo from the Pink Floyd song "Comfortably Numb" using the Karplus-Strong Algorithm.
To synthesize the guitar part of the song I wrote a modified version of the Karplus-Strong Algorithm - an algorithm for synthesizing the sound created by a plucked string. I made a few modifications to it to make the sound more realistic, which are described in detail below. Then I performed some post-processing on the guitar sound to make it sound like an electric guitar, including amplifier modeling, distortion and reverb. Finally, I used a basic MIDI file to synthesize the supporting instruments (drums, bass etc..).
I did the post-processing and instrument generation with a great, inexpensive Digital Audio Workstation (DAW) called Reaper.
Modifications to Karplus-Strong
To get a basic understanding of the Karplus-Strong algorithm, you can read about it here.
I made some modifications to the basic Karplus-Strong algorithm for my project. Most of them were inspired by this page by Nicholas P. Donaldson.
My modifications included: - A variable second-order low-pass loop filter - An all-pass filter with adjustable delay to allow for continuous frequency selection - A dynamic delay line length and all-pass filter delay to allow for glissandi (bends)
My final K-S implementation (after all modifications) looked like this:
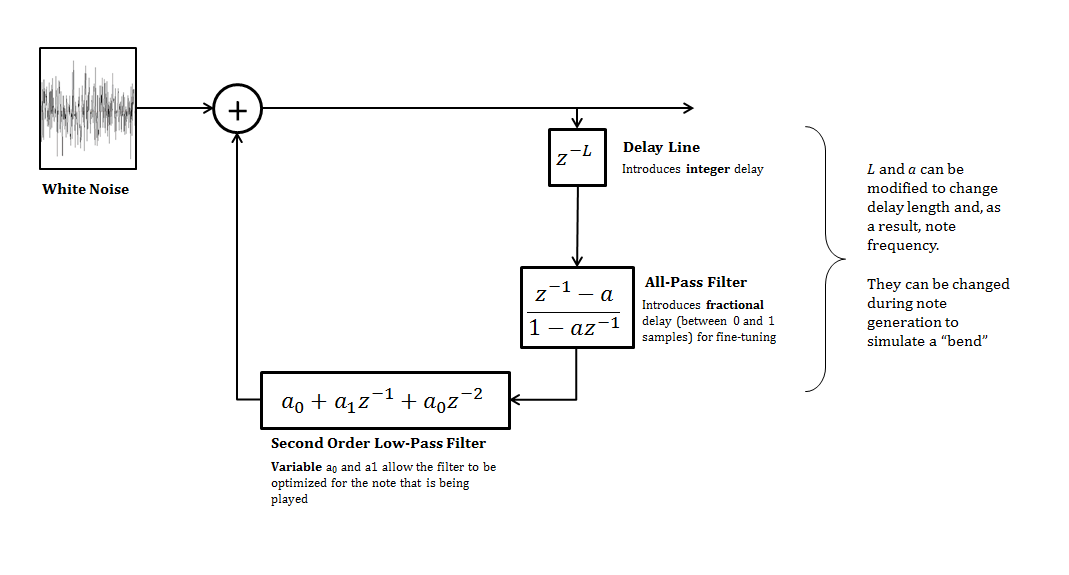
Low-Pass Filter
The original K-S implementation just uses a simple two-point averager for the Low-Pass filter, but I wanted something more configurable, so I used a second order filter as described by Donaldson:
A major problem this choice allowed me to solve is that of different notes decaying at different rates. Typically, K-S uses the same filter for every generated note. This means that higher notes get attenuated more by the low-pass filter and thus decay faster. This sounds very unrealistic, and I felt that it ruined my entire composition.
I was able to solve this problem by adusting the filter coefficients based on the frequency of the note being generated. I use the following design equations to compute these coefficients:
Where \(f_o\) is the note frequency and \(f_s\) is the sampling frequency (usually 44.1 kHz).
These equations configure the filter so that it has a gain of 0.999 at 4 times the note frequency. That setting is arbitrary, but I found that it gave me a good amount of sustain over the entire range of notes that I was generating.
All-Pass Filter
The original Karplus-Strong algorithm just used a delay line in the loop, but this only allows for a delay equal to an integer number of samples. To allow for finer delay adjustment, an all-pass filter is typically used. The all-pass filter introduces a fractional delay equal to \(1/a\), which, when combined with the integer delay of the delay line, allows for a very wide range of continuous delay adjustment.
Dynamic Delay
My implementation of the Karplus-Strong algorithm allows the delay line parameter, \(L\), and the all-pass filter parameter, \(a\), to be adjusted while the algorithm is running.
This dynamically adjusts the amount of delay in the loop, which adjusts the note frequency. Adjusting it during note generation creates a "bend".
The Result
I used my custom algorithm to synthesize the entire guitar part of the solo. I used Reaper to do a little bit of post processing on the track and added a few other instruments. You can listen to the final result below: